The Power of Compounding Interest

When you’re saving, the bank (or financial institution) adds interest to your savings at regular intervals (for example, every month). 

If you don’t touch the interest, but let it add to your lump sum, then you start to earn interest on your interest, as well as on the original amount you saved. This is called compound interest.

The longer you leave your money, the more powerful the compound interest effect. So the earlier you start saving, the more you make from compound interest. The same applies to other investments such as shares, where you regularly reinvest dividends, or the company reinvests its profits.

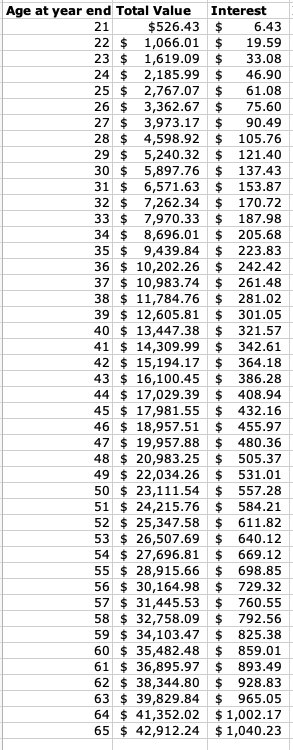
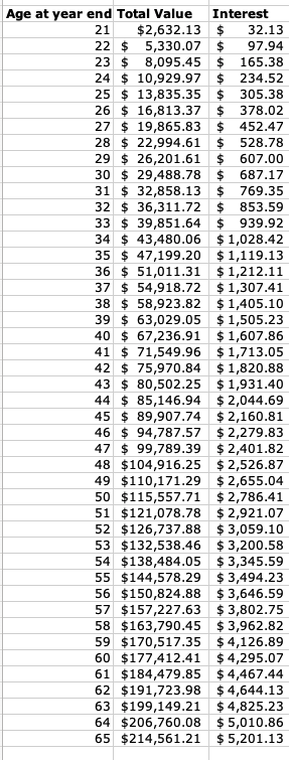
Consider the example of Viv. Viv’s a 20 year old who decides to start saving a regular amount each week. The tables below show how much she will end up with if she keeps up her saving (either $10 per week or $50 per week) until she is 65. We’ve based Viv’s results on an interest rate of 2.5% after tax and allowing for inflation.

We’ve also assumed that Viv will increase the amount she saves each week to account for inflation.
If inflation is 2% this year, Viv will increase her weekly savings by 2% from next year (from $50 to $51)

Look at the first five years and the last five years of the $10 table. In the first five years Viv saves $2,667 and earns $167 in interest. In the last five years, she’s still saving only $2,667, but she earns a massive $4,830 in interest – far more than she saves. That’s the power of compound interest!

For the $50  a week saving, for the first five years it is $835.35, and last five years $24,418.

The Rule of 72 

There’s an easy rule you can use to work out how your savings or investments can grow with compound interest. Just divide the interest rate (or average annual return) into 72. The result tells you how long it will take for your money to double without further savings.

For example, you have $10,000, which is earning 6% interest (after tax). 72 divided by 6 = 12. Every 12 years your $10,000 will double, so:

After 12 years you have $20,000
After 24 years you have $40,000
After 36 years you have $80,000

However, these dollar figures include the impact of inflation (so $80,000 in 36 years is not the same as $80,000 today). To be completely accurate in working out how much you would have to spend (compared to today), you would need to deduct something from the interest rate (this will allow for inflation). For example, if you allowed for 2% inflation, the real interest rate would be 4%.